Kd-Trees

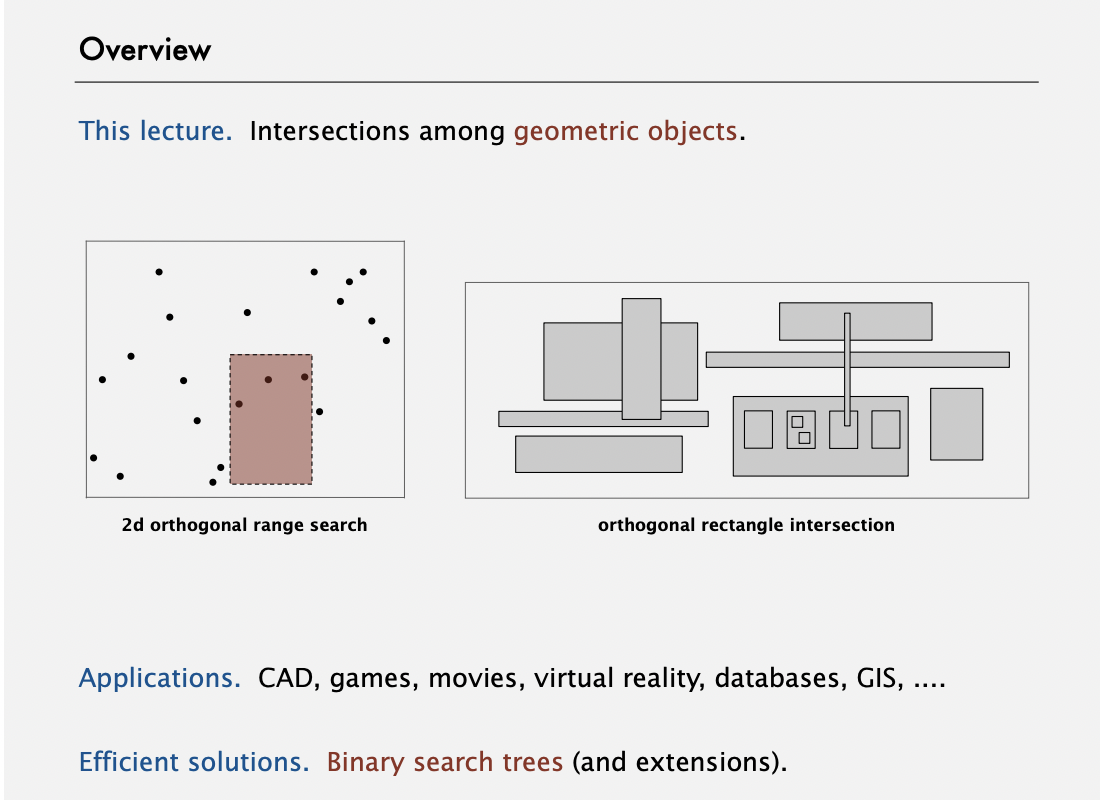
Geometric application of BSTs

1d range search

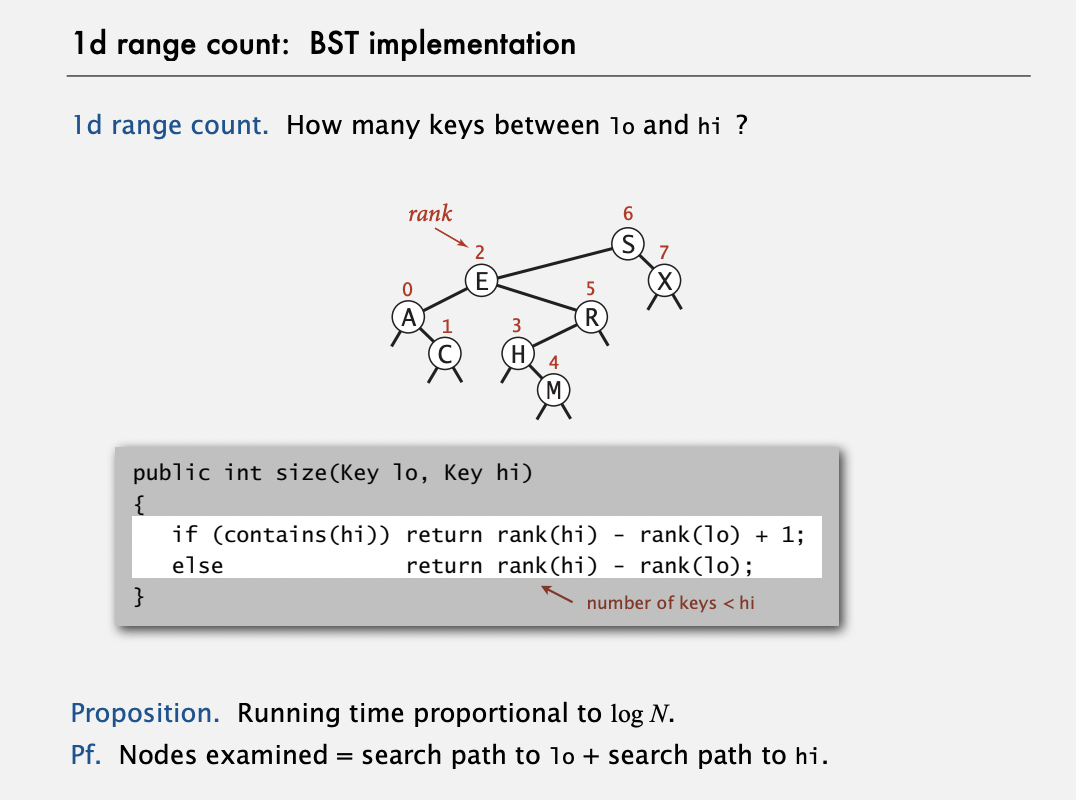
1d range count on BST can be achieved with recursive rank() calls.

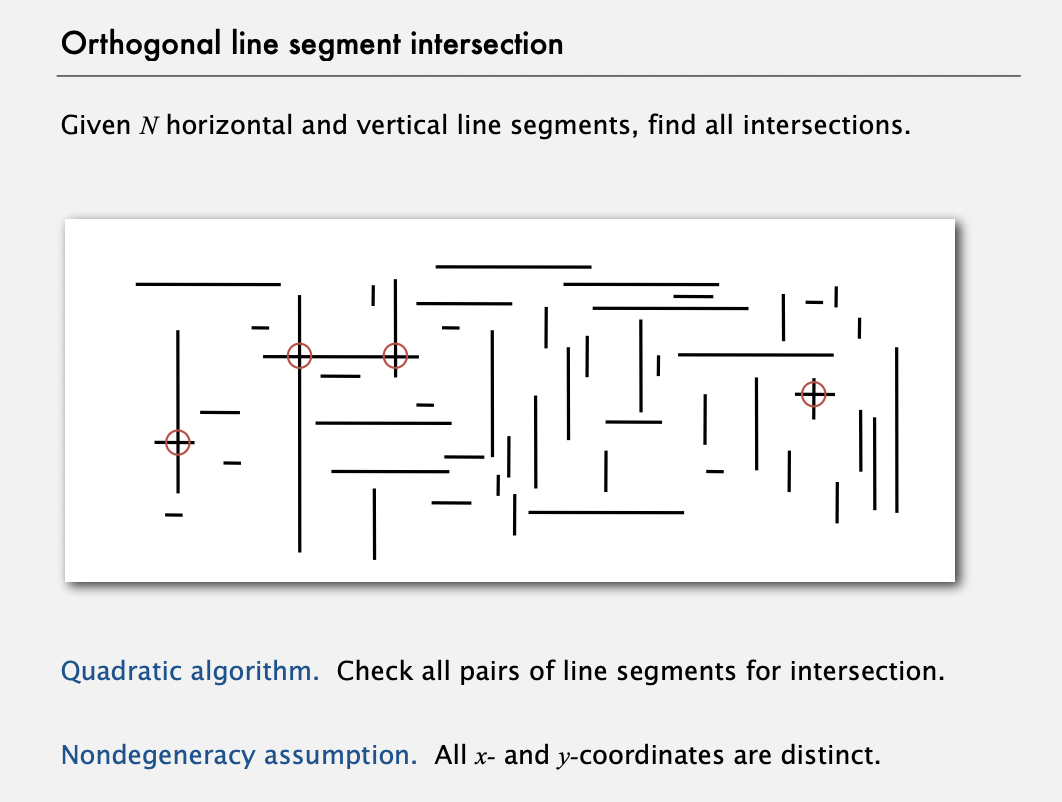
Orthogonal line segment intersection - sweep line algorithm

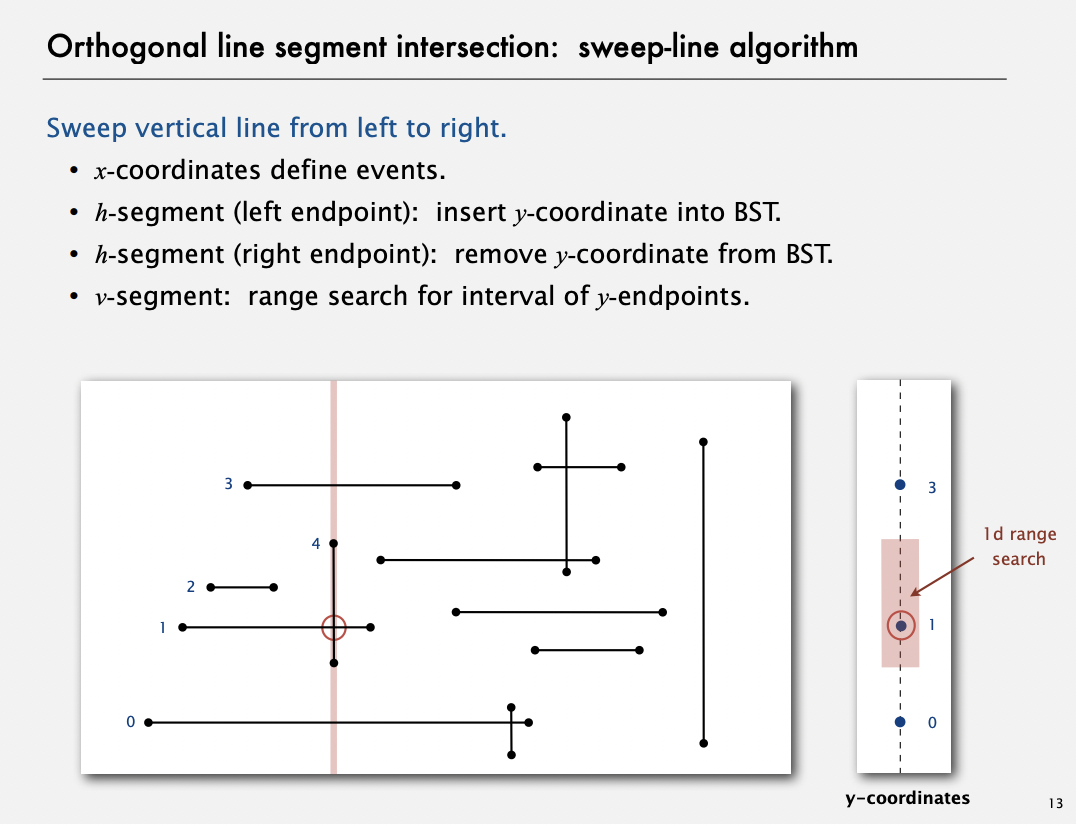
2-d orthogonal range search - Kd-trees

Kd tree: Recursively partition k-dimensional space into 2 halfspaces