Red-Black BSTs
Link to course presentations.
BTS - binary search tree is a very good data structure
that has fast insert and search property. One key point
in making a BST to work well for any cases is to keep
the tree balanced, or to keep the height of tree as
low as possible. This is achieved via algorithms such
as 2-3 tree and Red-Black tree (which is a different
representation of 2-3 tree).
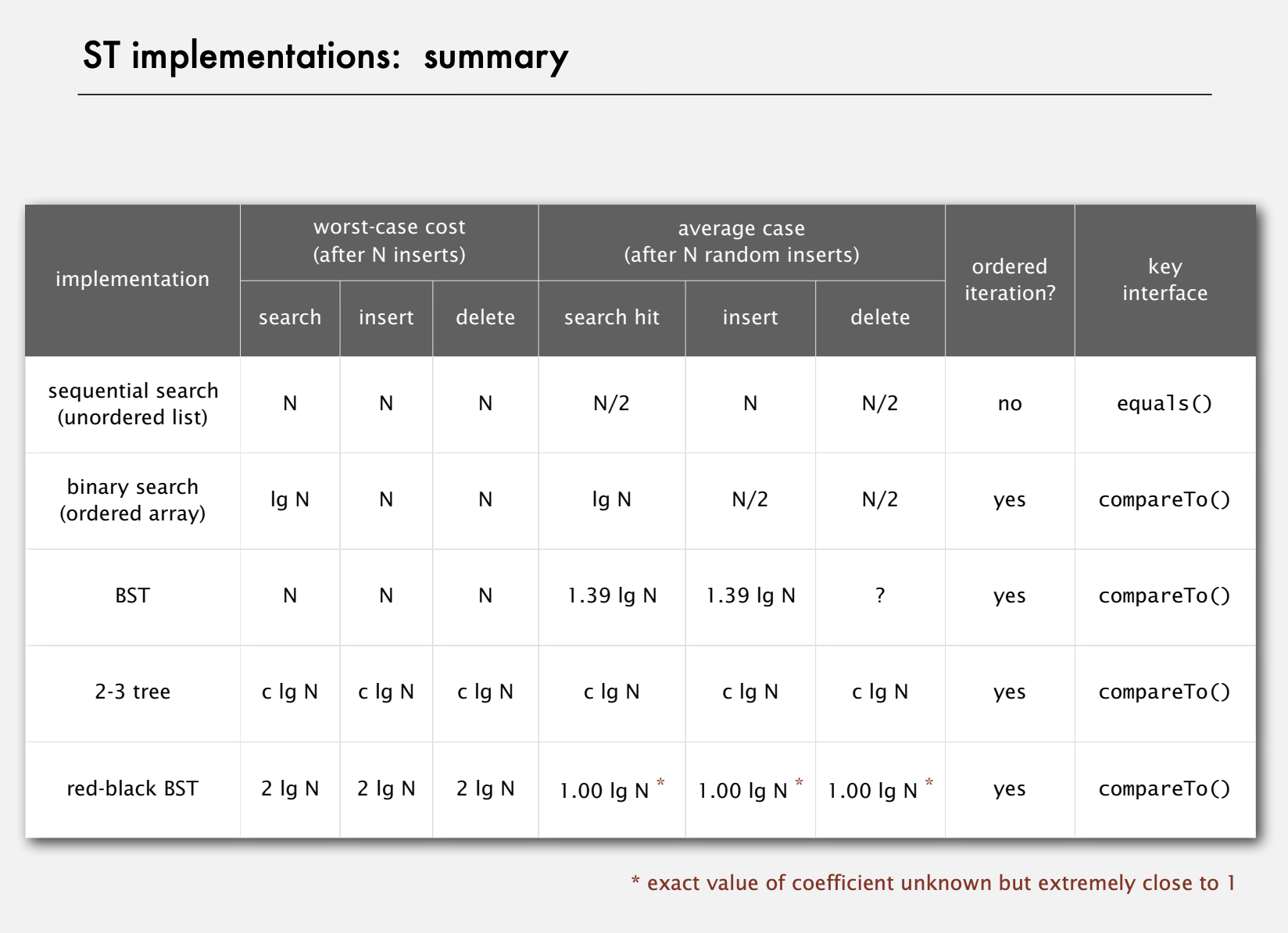
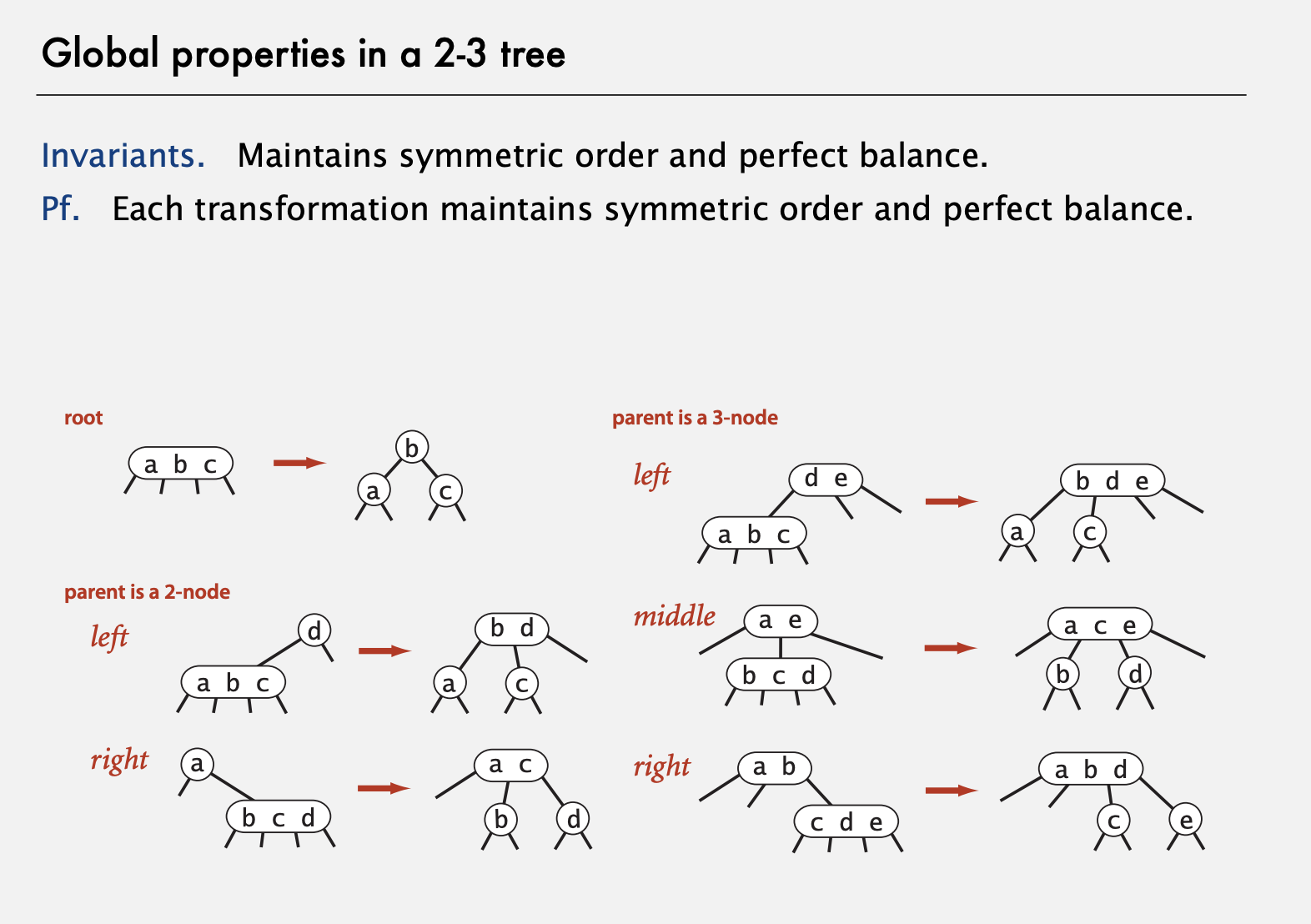
2-3 tree
Allow 1 or 2 keys per node.
- 2-node: one key, two children.
- 3-node: two keys, three children.
- 4-node: a special temporary condition, 4 children, only exist for a short time while inserting
Guaranteed logarithmic performance for search and insert, worst case: \(height \leq c log_{2}(n) \)
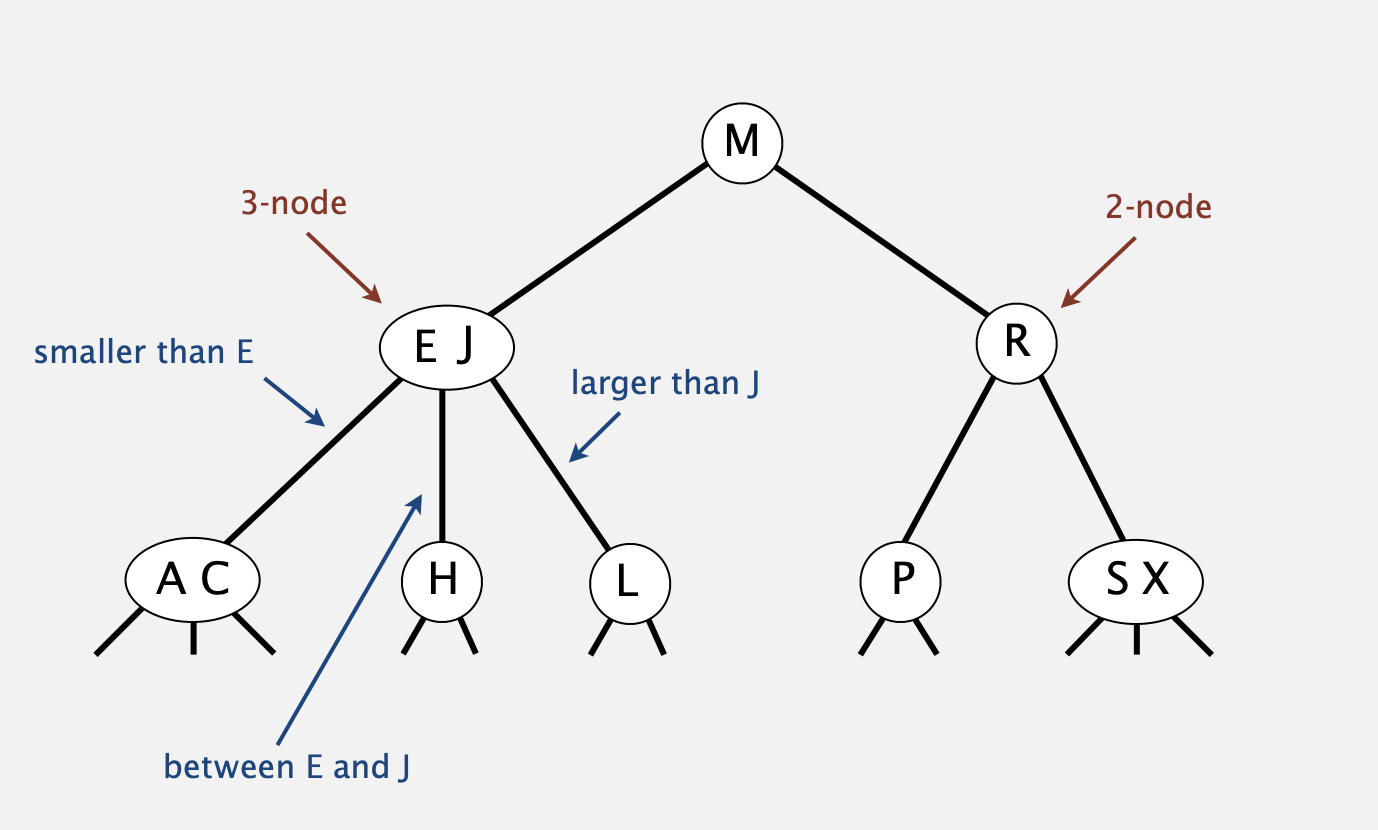
Insertion into a 3-node at bottom.
- Add new key to 3-node to create temporary 4-node.
- Move middle key in 4-node into parent.
- Repeat up the tree, as necessary.
- If you reach the root and it's a 4-node, split it into three 2-nodes.
Left-leaning red-black BSTs (Guibas-Sedgewick 1979 and Sedgewick 2007)
Idea: ensure that hight always O(log N) (best possible)
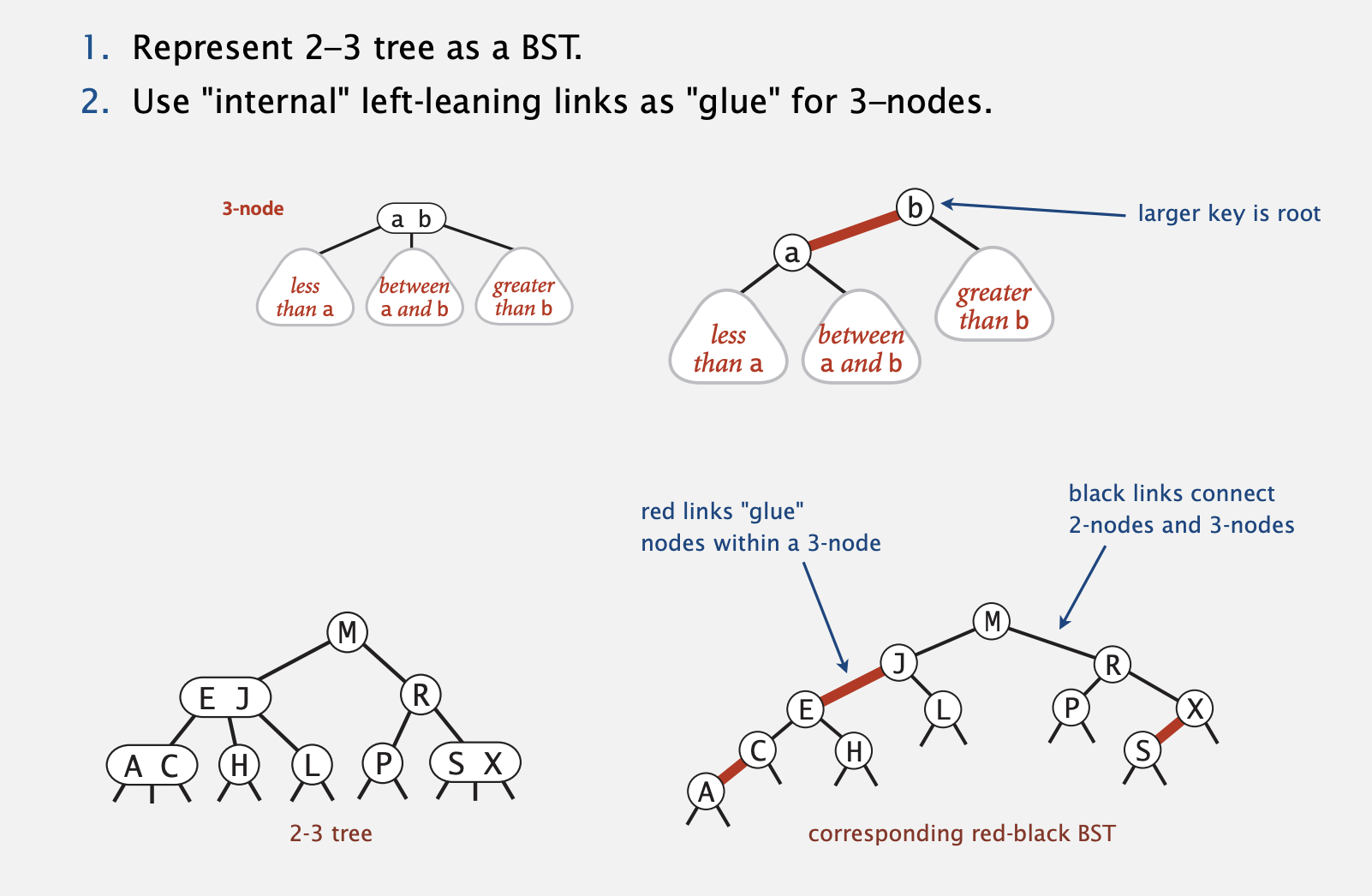
A Red-Black BST that has rules:
- each node
redorblack - root is always black
- no red nodes in a row
- red node => only black children
- every root-Null path (like in an unsuccessful search) has the same number of black nodes
- red links lean left
Left-leaning red-black BSTs: 1-1 correspondence with 2-3 trees
Hight Guarantee: if it is a red-black tree with n nodes, then it has \(height \leq 2 log_{2}(n + 1) \)
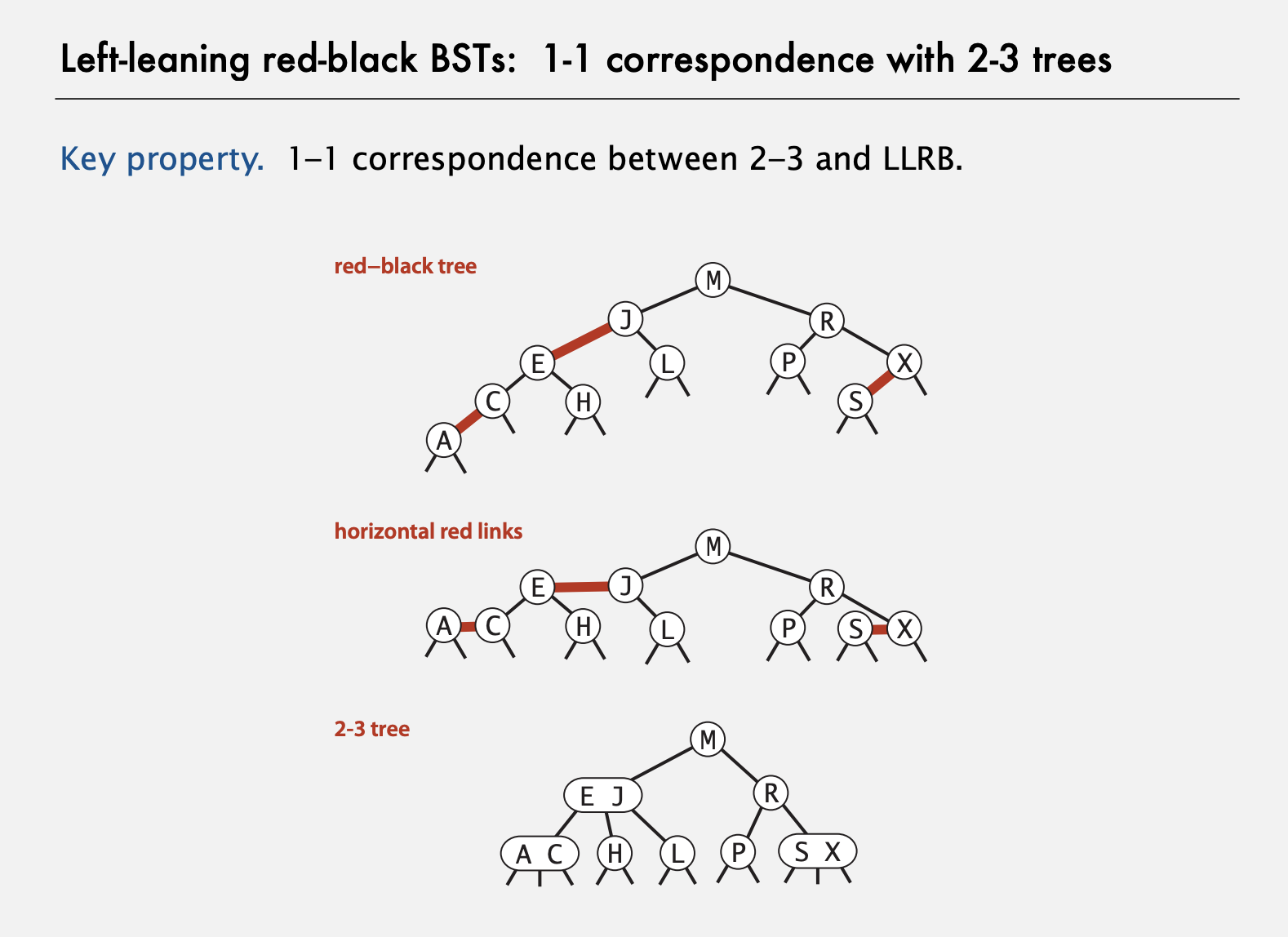
Every root to leaf path has the same number of black nodes
Sedgewick's friend wrote him a late night email telling him in this show they actually got the line for Red-Black tree correct. (And I don't think that helps with the ladies :) )
Click to see scripts...

Achieved by 3 basic operations
- Left Rotation
- Right Rotation
- Flip Colors